
🦀📐 Building a Linear Algebra Engine in Rust — Part 1
Beyond Frameworks, No Shortcuts
Everyone can import. Few can build. Let's change that.

Everyone can import. Few can build. Let's change that.
LinearAlgebra-WS is a transparent, minimal, and open-source linear algebra library built entirely in Rust by Willy Sajbeni. Ideal for students, researchers, engineers, and developers who value speed, privacy, and control.
cargo install linear_algebra_wslinear_algebra_ws
Most modern machine learning libraries (TensorFlow, PyTorch, etc.) embed telemetry and hidden behaviors. LinearAlgebra-WS is different — it's completely open, simple, transparent, and under your full control. No tracking. No hidden code. Just math.
After receiving hundreds of messages, questions, and pieces of advice — and being deeply grateful to the community — I decided to take a step back to leap much further ahead. This is the start of a long-term project: building, from scratch and without external libraries, everything behind what powers HFT, Machine Learning, Deep Learning, and AI today.
Linear Algebra is the foundation of nearly every operation in these fields. From strategy optimization in HFT to the inner workings of machine learning models and neural networks, vectors, matrices, and linear transformations are the core. Without a solid foundation at this level, everything else becomes a misunderstood black box.
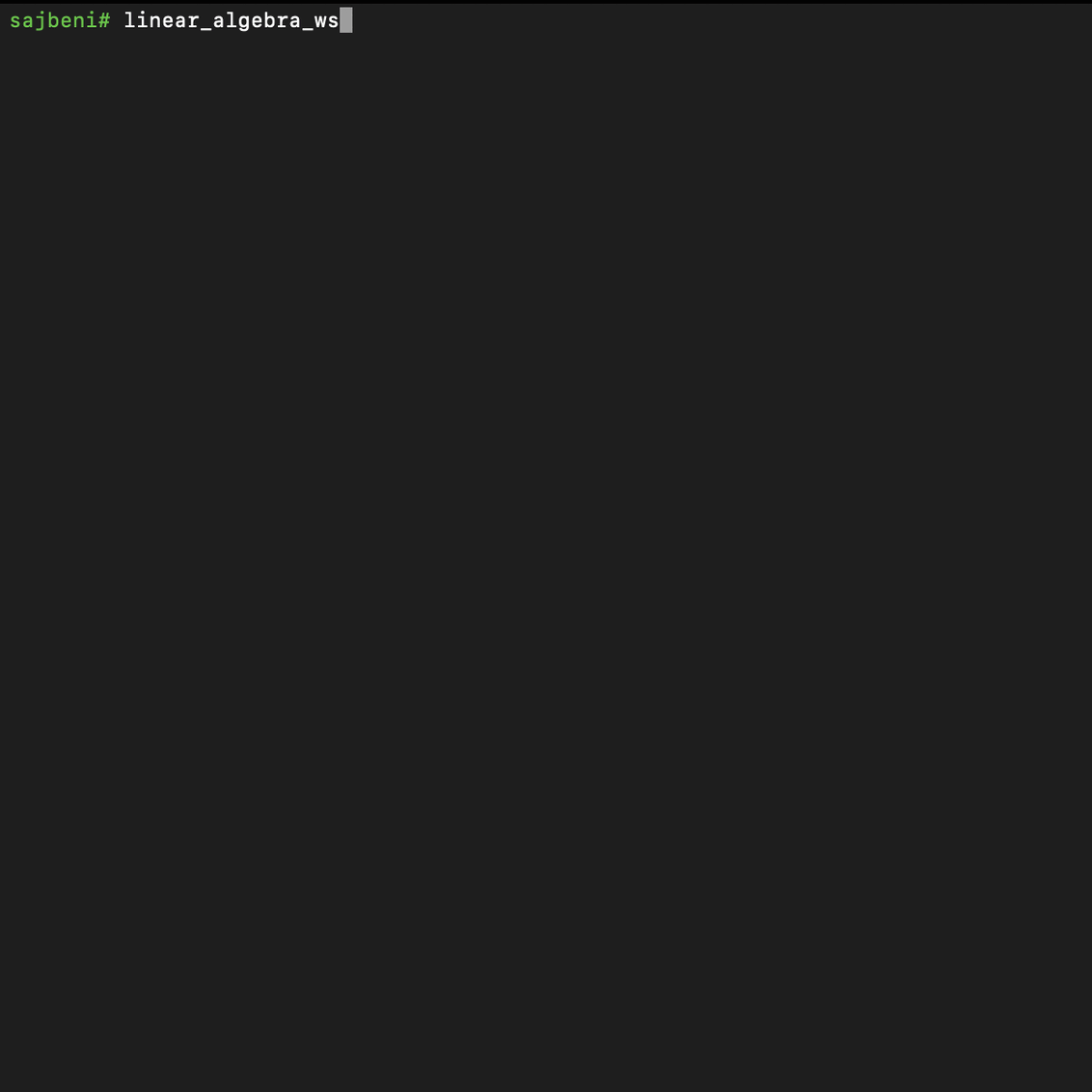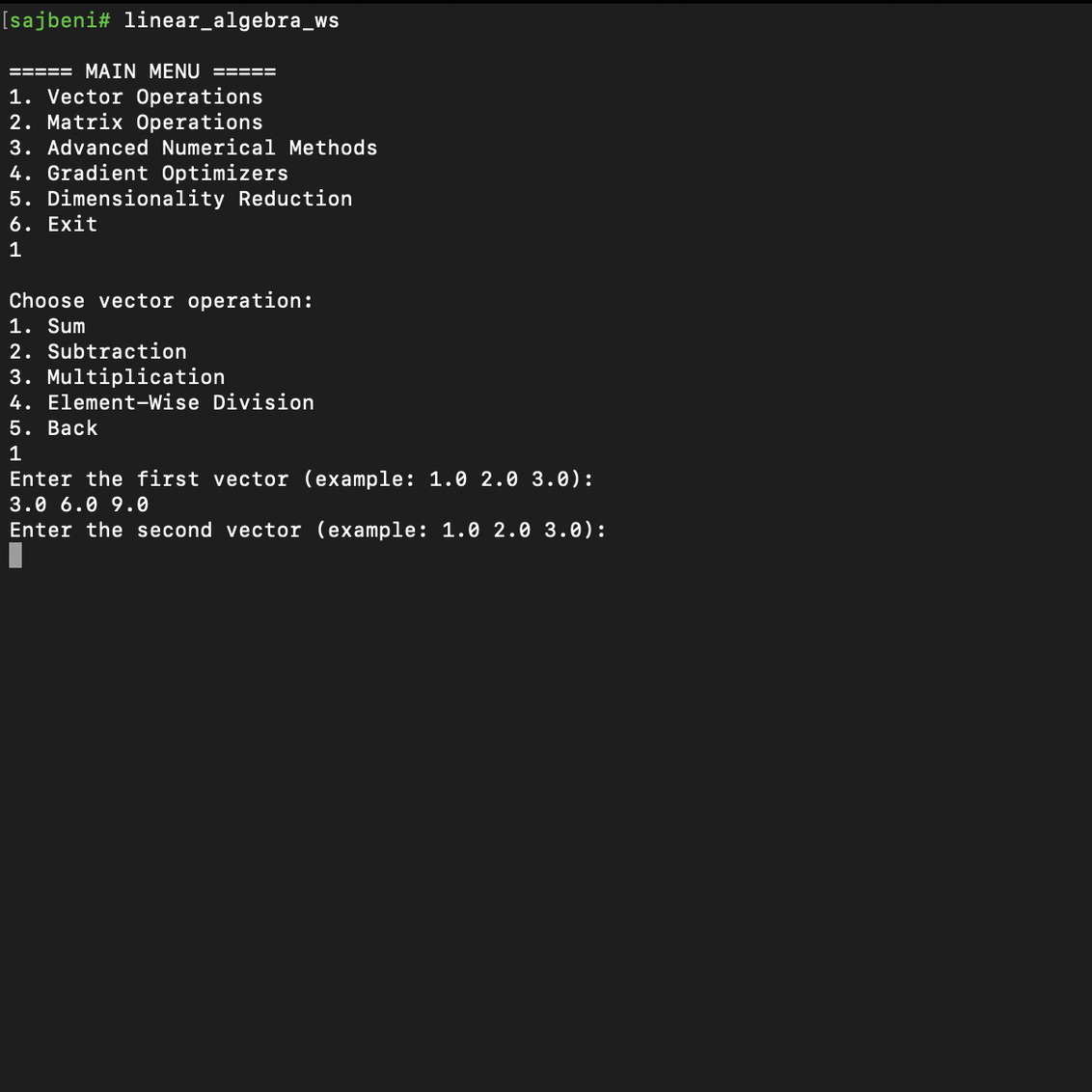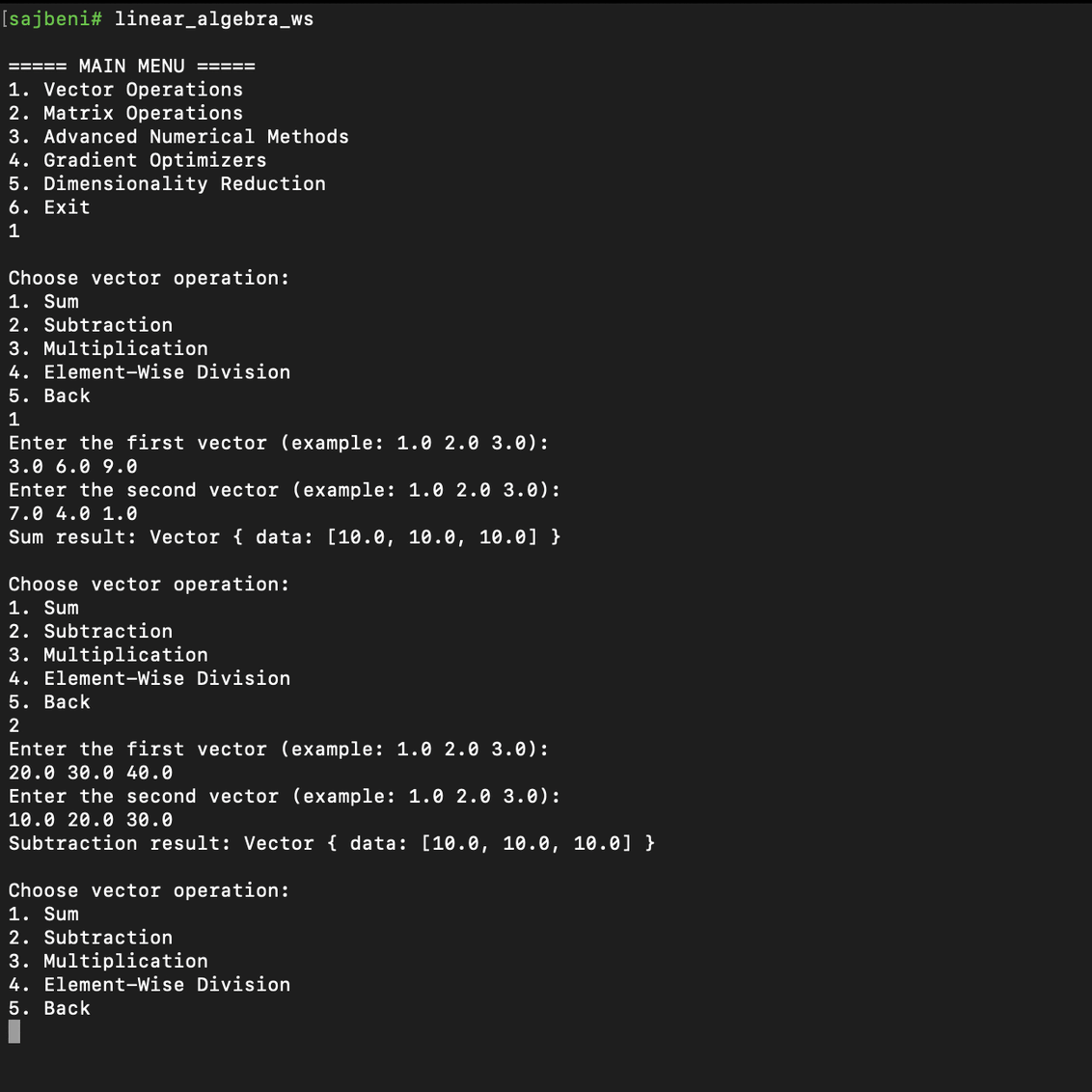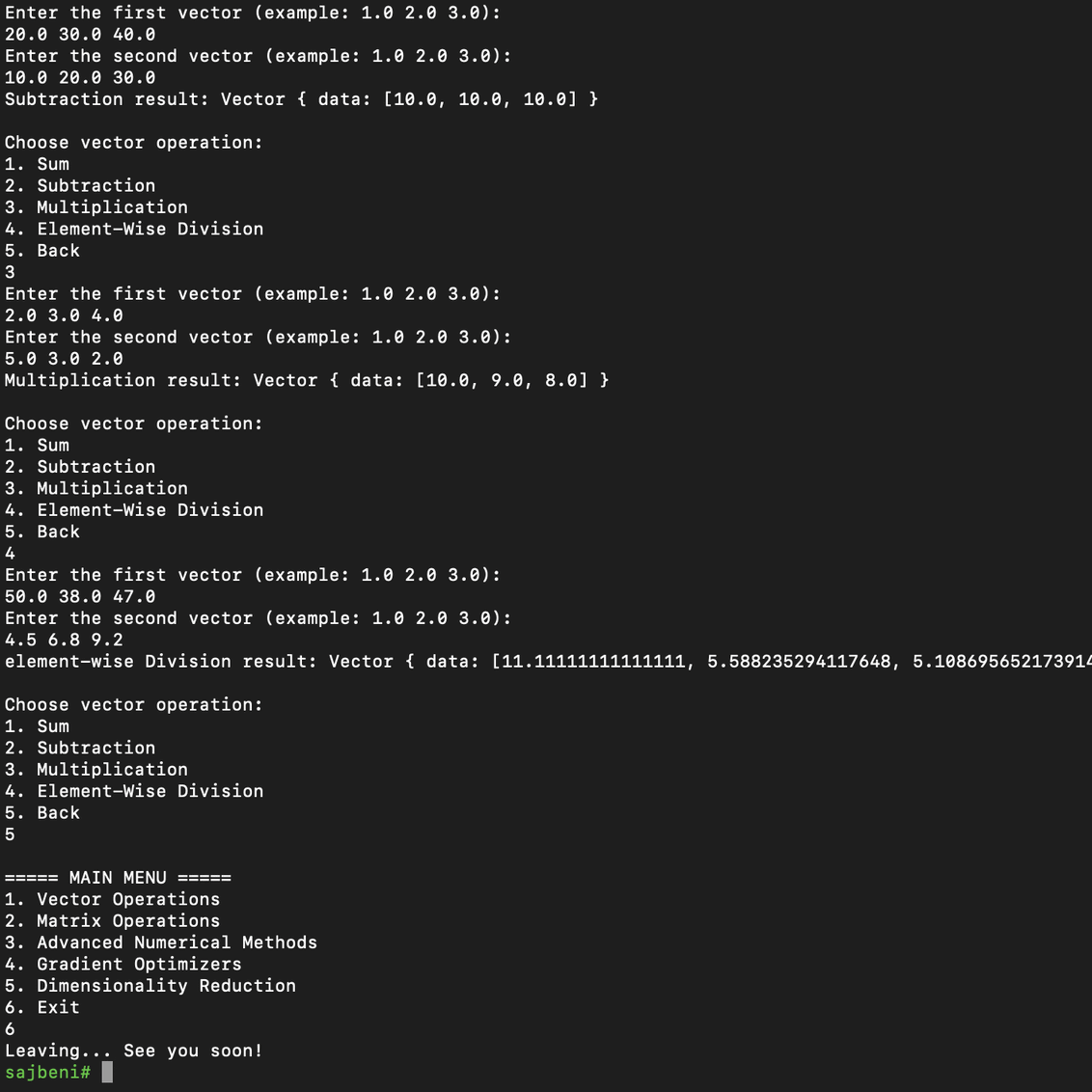
I have implemented basic vector operations (sum, subtraction, multiplication, element-wise division), which are fundamental for building more complex numerical engines.
Today, many data scientists and engineers know how to use pre-built frameworks but lack deep understanding of what happens internally. For example, TensorFlow is not truly Python — it’s a heavily optimized C++ core. Understanding these internals is the difference between being a user and a true builder of technology.
My goal is to build a "TensorFlow from scratch" and a complete HFT infrastructure from scratch. This requires patience, discipline, and a lot of study — but through this journey, we can achieve real excellence.
I chose Rust because it is the most brilliantly designed programming language today. It forces manual memory control, modular design, respect for ownership, and long-term system architecture thinking. The genius of the Rust community is visible in details like the "&" symbol, which forces explicit sharing and borrowing. This reduces memory usage, prevents duplication, increases speed, and eliminates garbage collection reliance — critical for fields like HFT and AI where every microsecond and byte matters.
This project is licensed under the MIT License.
Here’s a simple HFT-style simulation in Rust using threads and channels.
// linear_algebra_ws
// Author: Willy Sajbeni
// Website: https://www.sajbeni.com
// GitHub: https://github.com/willySajbeni
// LinkedIn: https://www.linkedin.com/in/willysajbeni/
// Email: willy@sajbeni.com
// Structure definition:
// A Vector will have a field called data, and this field is a Vec<f64>.
// When inserting a vector, the v1 object really exists, and v1.data has a Vec<f64> inside, e.g., [1.0, 2.0, 3.0].
// There, the 'let' binding is created.
#[derive(Debug)]
pub struct Vector {
data: Vec<f64>,
}
// We are implementing methods for the Vector type.
impl Vector {
pub fn new(data: Vec<f64>) -> Self {
Vector { data }
}
// Vector addition: v1 + v2 = [a1+b1, a2+b2, a3+b3]
// Creating a function called add:
pub fn add(&self, other: &Self) -> Self {
// - &self ➔ the vector that calls the method
// - &other ➔ another vector to add
// - Returns ➔ a new Vector
assert_eq(self.data.len(), other.data.len(), "Vectors must be the same size for addition.");
let data = self.data.iter()
.zip(&other.data)
.map(|(x, y)| x + y)
.collect();
Vector::new(data)
}
// Vector subtraction: v1 - v2 = [a1-b1, a2-b2, a3-b3]
// Creating a function called subtract:
pub fn subtract(&self, other: &Self) -> Self {
// - &self ➔ the vector that calls the method
// - &other ➔ another vector to subtract
// - Returns ➔ a new Vector
assert_eq(self.data.len(), other.data.len(), "Vectors must be the same size for subtraction.");
let data = self.data.iter()
.zip(&other.data)
.map(|(x, y)| x - y)
.collect();
Vector::new(data)
}
// Element-wise multiplication of vectors: v1 × v2 = [a1×b1, a2×b2, a3×b3]
// Creating a function called multiply:
pub fn multiply(&self, other: &Self) -> Self {
// - &self ➔ the vector that calls the method
// - &other ➔ another vector to multiply
// - Returns ➔ a new Vector
assert_eq(self.data.len(), other.data.len(), "Vectors must be the same size for multiplication.");
let data = self.data.iter()
.zip(&other.data)
.map(|(x, y)| x * y)
.collect();
Vector::new(data)
}
// Element-wise division of vectors (Multiplication by Inverse)
// Instead of traditional division, we multiply by the inverse of each element.
// Formula: v1 / v2 = [a1×(1/b1), a2×(1/b2), a3×(1/b3)]
// Important: Check for division by zero!
pub fn element_wise_division(&self, other: &Self) -> Self {
// Validate vectors are the same size
assert_eq(self.data.len(), other.data.len(), "Vectors must be the same size for division.");
// Ensure no division by zero
assert!(!other.data.iter().any(|&x| x == 0.0), "Cannot divide by zero.");
let data = self.data.iter()
.zip(&other.data)
.map(|(x, y)| x * (1.0 / y))
.collect();
Vector::new(data)
}
}
Vec<f64> as its data.zip, and map for clean, efficient computation.Linear Algebra is the true foundation behind high-frequency trading, machine learning, deep learning, and artificial intelligence. With LinearAlgebra-WS, we return to the roots — building mathematics from scratch, without black boxes, with full transparency and control.
This is just the beginning: mastering basic vector operations unlocks the door to deeper and more powerful numerical computation. By understanding these core structures, we can move beyond using frameworks and start truly creating the next generation of intelligent systems.
In future updates, we'll expand into matrix operations, optimizers, dimensionality reduction, and more — all in pure Rust, fully open source, and ready for real-world HFT, ML, DL, and AI challenges.
Let's rebuild the future, one vector at a time. 🦀📐